Solves the empirical Bayes normal means (EBNM) problem using a specified family of priors. For a detailed introduction to the package, see Willwerscheid, Carbonetto, and Stephens (2025), our JSS article cited in References below.
ebnm(
x,
s = 1,
prior_family = c("point_normal", "point_laplace", "point_exponential", "normal",
"horseshoe", "normal_scale_mixture", "unimodal", "unimodal_symmetric",
"unimodal_nonnegative", "unimodal_nonpositive", "generalized_binary", "npmle",
"deconvolver", "flat", "point_mass", "ash"),
mode = 0,
scale = "estimate",
g_init = NULL,
fix_g = FALSE,
output = ebnm_output_default(),
optmethod = NULL,
control = NULL,
...
)
ebnm_output_default()
ebnm_output_all()Arguments
- x
A vector of observations. Missing observations (
NAs) are not allowed.- s
A vector of standard errors (or a scalar if all are equal). Standard errors may not be exactly zero, and missing standard errors are not allowed. Two prior families have additional restrictions: when horseshoe priors are used, errors must be homoskedastic; and since function
deconvin packagedeconvolveRtakes \(z\)-scores, the "deconvolver" family requires that all standard errors be equal to 1.- prior_family
A character string that specifies the prior family \(G\). See Details below.
- mode
A scalar specifying the mode of the prior \(g\) or
"estimate"if the mode is to be estimated from the data. This parameter is ignored by the NPMLE, thedeconvolveRfamily, and the improper uniform (or "flat") prior. For generalized binary priors, which are bimodal, the mode parameter specifies the mode of the truncated normal component (the location of the point mass is fixed at zero).- scale
A scalar or vector specifying the scale parameter(s) of the prior or
"estimate"if the scale parameters are to be estimated from the data. This parameter is ignored by the flat prior and the family of point mass priors.The interpretation of
scaledepends on the prior family. For normal and point-normal families, it is a scalar specifying the standard deviation of the normal component. For point-Laplace and point-exponential families, it is a scalar specifying the scale parameter of the Laplace or exponential component. For the horseshoe family, it corresponds to \(s\tau\) in the usual parametrization of thehorseshoedistribution. For the family of generalized binary priors, it specifies the ratio of the (untruncated) standard deviation of the normal component to its mode. This ratio must be fixed in advance (i.e., argument"estimate"is unavailable for generalized binary priors). For the NPMLE anddeconvolveRprior family,scaleis a scalar specifying the distance between successive means in the grid of point masses or normal distributions used to estimate \(g\). For all other prior families, which are implemented using the functionashin packageashr, it is a vector specifying the parametermixsdto be passed toashor"estimate"ifmixsdis to be chosen byebnm. (Note thatebnmchoosesmixsddifferently fromash: see functionsebnm_scale_normalmix,ebnm_scale_unimix, andebnm_scale_npmlefor details. To use theashgrid, setscale = "estimate"and pass ingridmultas an additional parameter. Seeashfor defaults and details.)- g_init
The prior distribution \(g\). Usually this is left unspecified (
NULL) and estimated from the data. However, it can be used in conjuction withfix_g = TRUEto fix the prior (useful, for example, to do computations with the "true" \(g\) in simulations). Ifg_initis specified butfix_g = FALSE,g_initspecifies the initial value of \(g\) used during optimization. For non-parametric priors, this has the side effect of fixing themodeandscaleparameters. Ifg_initis supplied, it should be an object of classnormalmixfor normal, point-normal, scale mixture of normals, anddeconvolveRprior families, as well as for the NPMLE; classlaplacemixfor point-Laplace families; classgammamixfor point-exponential families; classhorseshoefor horseshoe families; classunimixforunimodal_families; or classtnormalmixfor generalized binary priors. An object of classebnmcan also be supplied as argument, provided that fieldfitted_gcontains a prior of the correct class (see Examples below).- fix_g
If
TRUE, fix the prior \(g\) atg_initinstead of estimating it.- output
A character vector indicating which values are to be returned. Function
ebnm_output_default()provides the default return values, whileebnm_output_all()lists all possible return values. See Value below.- optmethod
A string specifying which optimization function is to be used.
For parametric families other than the horseshoe and generalized binary (normal, point-normal, point-Laplace, and point-exponential), options include
"nlm"(which callsnlm),"lbfgsb"(which callsoptimwithmethod = "L-BFGS-B"), and"trust"(which calls into thetrustpackage). Other options are"nohess_nlm","nograd_nlm", and"nograd_lbfgsb", which use numerical approximations rather than exact expressions for the Hessian; both of the"nograd"functions use numerical approximations for the gradient as well. The default option is"nohess_nlm".Since the horseshoe, generalized binary, and point mass families only require one parameter to be estimated (at most), the only available optimization method is
optimize, and thus theoptmethodparameter is ignored byebnm_horseshoe,ebnm_generalized_binary, andebnm_point_mass.For most nonparametric families (scale mixtures of normals; unimodal, symmetric unimodal, nonnegative unimodal, and nonpositive unimodal families; and the NPMLE),
optmethodoptions are provided by packageashr. The default method uses the mix-SQP algorithm implemented in themixsqppackage. See theashfunction documentation for other options. For the NPMLE only, it is also possible to specifyoptmethod = "REBayes", which uses functionGLmixin theREBayespackage to estimate the NPMLE rather than using theashrpackage. Note thatREBayesrequires installation of the commercial interior-point solver MOSEK; for details, see the documentation forREBayesfunctionKWDual.The nonparametric exception is the the "deconvolveR" family. Since the
deconvolveRpackage only ever usesnlm,ebnm_deconvolverignores theoptmethodparameter.- control
A list of control parameters to be passed to the optimization function specified by parameter
optmethod.- ...
Additional parameters. When a
unimodal_prior family is used, these parameters are passed to functionashin packageashr. Although it does not call intoashr, the scale mixture of normals family accepts parametergridmultfor purposes of comparison. Whengridmultis set, anashr-style grid will be used instead of the defaultebnmgrid. When the "deconvolver" family is used, additional parameters are passed to functiondeconvin packagedeconvolveR. Families of generalized binary priors take several additional parameters; seeebnm_generalized_binary. In all other cases, additional parameters are ignored.
Value
An ebnm object. Depending on the argument to output, the
object is a list containing elements:
dataA data frame containing the observations
xand standard errorss.posteriorA data frame of summary results (posterior means, standard deviations, second moments, and local false sign rates).
fitted_gThe fitted prior \(\hat{g}\) (an object of class
normalmix,laplacemix,gammamix,unimix,tnormalmix, orhorseshoe).log_likelihoodThe optimal log likelihood attained, \(L(\hat{g})\).
posterior_samplerA function that can be used to produce samples from the posterior. For all prior families other than the horseshoe, the sampler takes a single parameter
nsamp, the number of posterior samples to return per observation. Sinceebnm_horseshoereturns an MCMC sampler, it additionally takes parameterburn, the number of burn-in samples to discard.
S3 methods coef, confint, fitted, logLik,
nobs, plot, predict, print, quantile,
residuals, simulate, summary, and vcov
have been implemented for ebnm objects. For details, see the
respective help pages, linked below under See Also.
Details
Given vectors of data x and standard errors s, ebnm
solves the "empirical Bayes normal means" (EBNM) problem for various
choices of prior family.
The model is $$x_j | \theta_j, s_j \sim N(\theta_j, s_j^2)$$
$$\theta_j \sim g \in G,$$ where \(g\), which is referred to as the
"prior distribution" for \(\theta\), is to be estimated from among
some specified family of prior distributions \(G\). Several options
for \(G\) are implemented, some parametric and others non-parametric;
see below for examples.
Solving the EBNM problem involves two steps. First, \(g \in G\) is estimated via maximum marginal likelihood: $$\hat{g} := \arg\max_{g \in G} L(g),$$ where $$L(g) := \prod_j \int p(x_j | \theta_j, s_j) g(d\theta_j).$$ Second, posterior distributions \(p(\theta_j | x_j, s_j, \hat{g})\) and/or summaries such as posterior means and posterior second moments are computed.
Implemented prior families include:
point_normalThe family of mixtures where one component is a point mass at \(\mu\) and the other is a normal distribution centered at \(\mu\).
point_laplaceThe family of mixtures where one component is a point mass at \(\mu\) and the other is a double-exponential distribution centered at \(\mu\).
point_exponentialThe family of mixtures where one component is a point mass at \(\mu\) and the other is a (nonnegative) exponential distribution with mode \(\mu\).
normalThe family of normal distributions.
horseshoeThe family of horseshoe distributions.
normal_scale_mixtureThe family of scale mixtures of normals.
unimodalThe family of all unimodal distributions.
unimodal_symmetricThe family of symmetric unimodal distributions.
unimodal_nonnegativeThe family of unimodal distributions with support constrained to be greater than the mode.
unimodal_nonpositiveThe family of unimodal distributions with support constrained to be less than the mode.
generalized_binaryThe family of mixtures where one component is a point mass at zero and the other is a truncated normal distribution with lower bound zero and nonzero mode. See Liu et al. (2023), cited in References below.
npmleThe family of all distributions.
deconvolverA non-parametric exponential family with a natural spline basis. Like
npmle, there is no unimodal assumption, but whereasnpmleproduces spiky estimates for \(g\),deconvolverestimates are much more regular. SeedeconvolveR-packagefor details and references.flatThe "non-informative" improper uniform prior, which yields posteriors $$\theta_j | x_j, s_j \sim N(x_j, s_j^2).$$
point_massThe family of point masses \(\delta_\mu\). Posteriors are point masses at \(\mu\).
ashCalls into function
ashin packageashr. Can be used to make direct comparisons ofebnmandashrimplementations of prior families such as scale mixtures of normals and the NPMLE.
Functions
ebnm_output_default(): Lists the default return values.ebnm_output_all(): Lists all valid return values.
References
Jason Willwerscheid, Peter Carbonetto, and Matthew Stephens (2025).
ebnm: an R Package for solving the empirical Bayes
normal means problem using a variety of prior families. Journal of
Statistical Software, 114(3), 1–33.
doi:10.18637/jss.v114.i03
.
Yusha Liu, Peter Carbonetto, Jason Willwerscheid, Scott A Oakes, Kay F Macleod, and Matthew Stephens (2025). Dissecting tumor transcriptional heterogeneity from single-cell RNA-seq data by generalized binary covariance decomposition. Nature Genetics 57, 263–273. doi:10.1038/s41588-024-01997-z .
See also
A plotting method is available for ebnm objects: see
plot.ebnm.
For other methods, see coef.ebnm, confint.ebnm,
fitted.ebnm, logLik.ebnm,
nobs.ebnm, predict.ebnm,
print.ebnm, print.summary.ebnm,
quantile.ebnm, residuals.ebnm,
simulate.ebnm,
summary.ebnm, and vcov.ebnm.
Calling into functions ebnm_point_normal,
ebnm_point_laplace,
ebnm_point_exponential, ebnm_normal,
ebnm_horseshoe,
ebnm_normal_scale_mixture, ebnm_unimodal,
ebnm_unimodal_symmetric,
ebnm_unimodal_nonnegative,
ebnm_unimodal_nonpositive,
ebnm_generalized_binary, ebnm_npmle,
ebnm_deconvolver, ebnm_flat,
ebnm_point_mass, and ebnm_ash
is equivalent to calling into ebnm with prior_family set
accordingly.
Examples
theta <- c(rep(0, 100), rexp(100))
s <- 1
x <- theta + rnorm(200, 0, s)
# The following are equivalent:
pn.res <- ebnm(x, s, prior_family = "point_normal")
pn.res <- ebnm_point_normal(x, s)
# Inspect results:
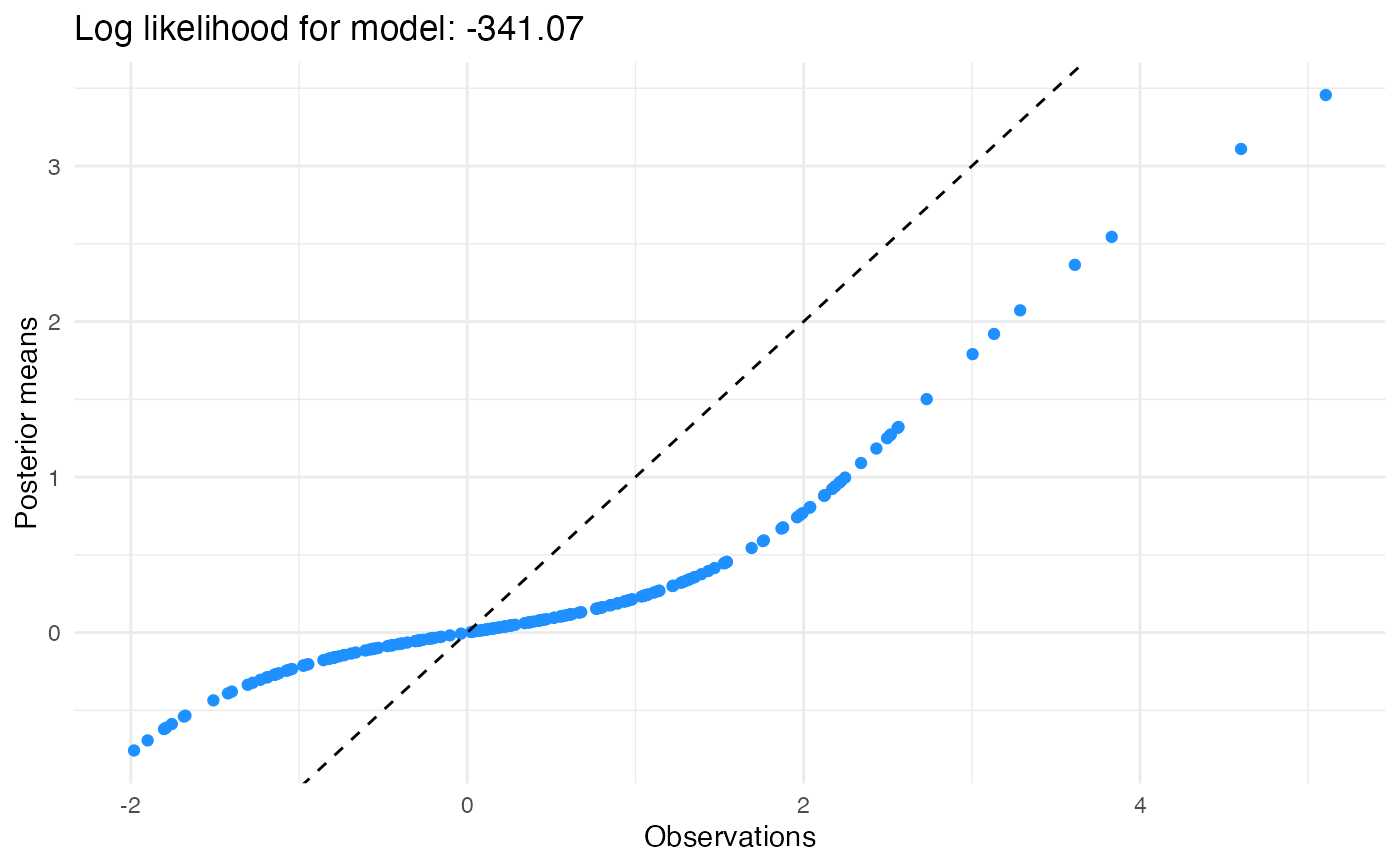
logLik(pn.res)
#> 'log Lik.' -343.8873 (df=2)
plot(pn.res)
 # Fix the scale parameter:
pl.res <- ebnm_point_laplace(x, s, scale = 1)
# Estimate the mode:
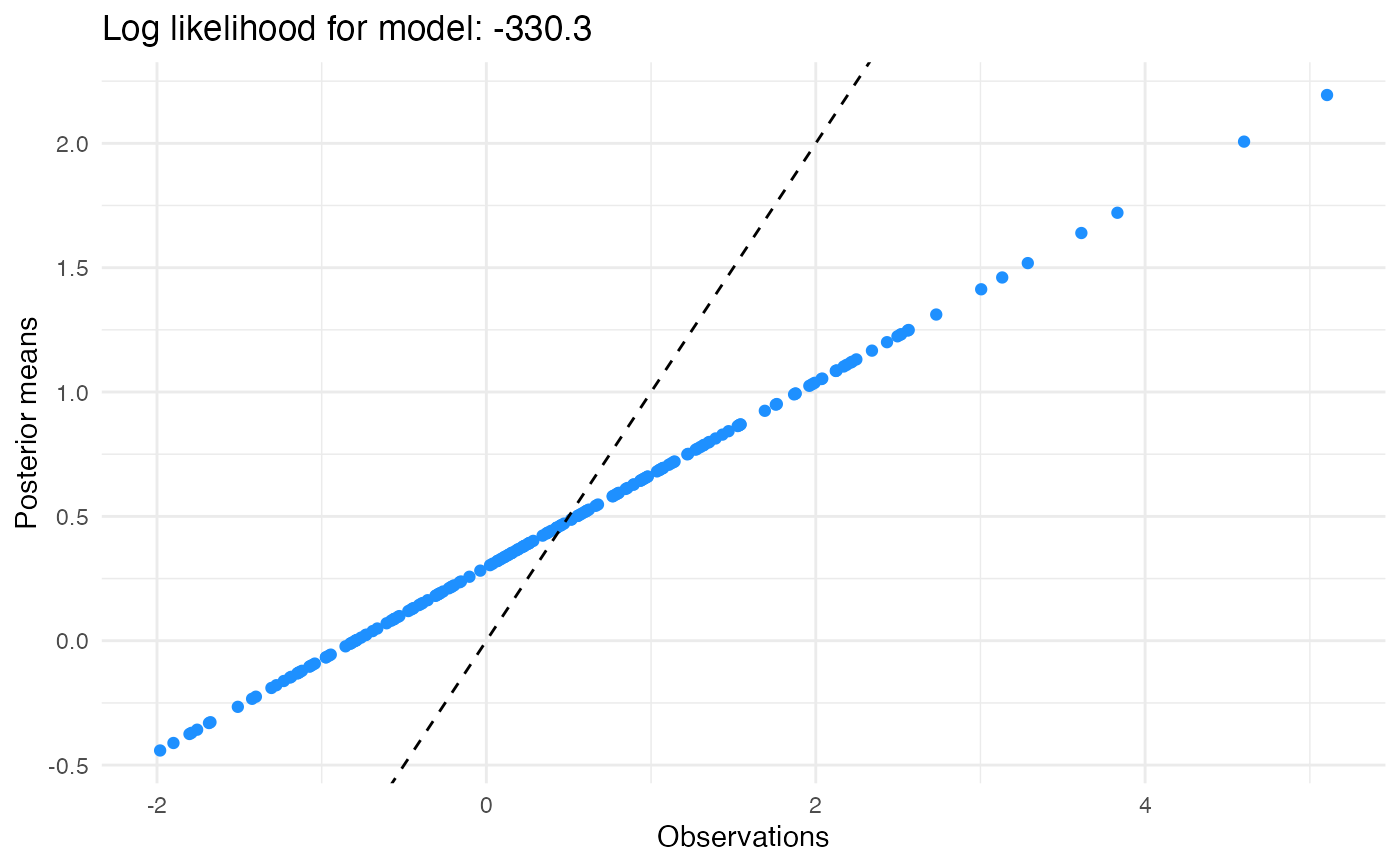
normal.res <- ebnm_normal(x, s, mode = "estimate")
plot(normal.res) # posterior means shrink to a value different from zero
# Fix the scale parameter:
pl.res <- ebnm_point_laplace(x, s, scale = 1)
# Estimate the mode:
normal.res <- ebnm_normal(x, s, mode = "estimate")
plot(normal.res) # posterior means shrink to a value different from zero
 # Use an initial g (this fixes mode and scale for ash priors):
normalmix.res <- ebnm_normal_scale_mixture(x, s, g_init = pn.res)
# Fix g and get different output (including a posterior sampler):
pn.res <- ebnm_point_normal(x, s, g_init = pn.res, fix_g = TRUE,
output = ebnm_output_all())
# Sample from the posterior:
pn.samp <- simulate(pn.res, nsim = 100)
# Quantiles and HPD confidence intervals can be obtained via sampling:
set.seed(1)
pn.quantiles <- quantile(pn.res, probs = c(0.1, 0.9))
pn.quantiles[1:5, ]
#> 10% 90%
#> [1,] 0.0000000 1.1914106
#> [2,] -1.0619459 0.1206053
#> [3,] 0.0000000 1.7507120
#> [4,] -0.1512883 0.9017663
#> [5,] 0.0000000 1.2735313
confint(pn.res, level = 0.8, parm = 1:5)
#> CI.lower CI.upper
#> [1,] -0.03860609 1.22003099
#> [2,] -1.05387886 0.06733079
#> [3,] -0.05568353 1.55045799
#> [4,] -0.06929657 1.08525964
#> [5,] -0.03277069 1.27950472
# Examples of usage of control parameter:
# point_normal uses nlm:
pn.res <- ebnm_point_normal(x, s, control = list(print.level = 1))
#> iteration = 0
#> Step:
#> [1] 0 0
#> Parameter:
#> [1] 0.0000000 0.6123253
#> Function Value
#> [1] 160.1828
#> Gradient:
#> [1] -0.6458203 1.6594072
#>
#> iteration = 5
#> Parameter:
#> [1] -0.06634847 0.48643374
#> Function Value
#> [1] 160.0995
#> Gradient:
#> [1] 5.052228e-06 -5.652389e-06
#>
#> Relative gradient close to zero.
#> Current iterate is probably solution.
#>
# unimodal uses mixsqp:
unimodal.res <- ebnm_unimodal(x, s, control = list(verbose = TRUE))
#> Running mix-SQP algorithm 0.3-54 on 201 x 7 matrix
#> convergence tol. (SQP): 1.0e-08
#> conv. tol. (active-set): 1.0e-10
#> zero threshold (solution): 1.0e-08
#> zero thresh. (search dir.): 1.0e-14
#> l.s. sufficient decrease: 1.0e-02
#> step size reduction factor: 7.5e-01
#> minimum step size: 1.0e-08
#> max. iter (SQP): 1000
#> max. iter (active-set): 8
#> number of EM iterations: 20
#> Computing SVD of 201 x 7 matrix.
#> Matrix is not low-rank; falling back to full matrix.
#> iter objective max(rdual) nnz stepsize max.diff nqp nls
#> 1 +7.073053156e-01 -- EM -- 7 1.00e+00 1.02e-01 -- --
#> 2 +6.300507676e-01 -- EM -- 7 1.00e+00 9.84e-02 -- --
#> 3 +5.856263291e-01 -- EM -- 7 1.00e+00 8.30e-02 -- --
#> 4 +5.605377271e-01 -- EM -- 7 1.00e+00 6.48e-02 -- --
#> 5 +5.463980593e-01 -- EM -- 7 1.00e+00 4.86e-02 -- --
#> 6 +5.383344434e-01 -- EM -- 7 1.00e+00 3.59e-02 -- --
#> 7 +5.336431001e-01 -- EM -- 7 1.00e+00 2.65e-02 -- --
#> 8 +5.308472577e-01 -- EM -- 7 1.00e+00 1.96e-02 -- --
#> 9 +5.291369016e-01 -- EM -- 7 1.00e+00 1.46e-02 -- --
#> 10 +5.280610563e-01 -- EM -- 7 1.00e+00 1.09e-02 -- --
#> 11 +5.273636428e-01 -- EM -- 7 1.00e+00 8.23e-03 -- --
#> 12 +5.268961570e-01 -- EM -- 7 1.00e+00 6.26e-03 -- --
#> 13 +5.265707094e-01 -- EM -- 7 1.00e+00 4.80e-03 -- --
#> 14 +5.263343276e-01 -- EM -- 7 1.00e+00 3.71e-03 -- --
#> 15 +5.261546016e-01 -- EM -- 7 1.00e+00 2.89e-03 -- --
#> 16 +5.260114829e-01 -- EM -- 7 1.00e+00 2.28e-03 -- --
#> 17 +5.258924899e-01 -- EM -- 7 1.00e+00 1.81e-03 -- --
#> 18 +5.257898363e-01 -- EM -- 7 1.00e+00 1.46e-03 -- --
#> 19 +5.256986728e-01 -- EM -- 7 1.00e+00 1.19e-03 -- --
#> 20 +5.256159886e-01 -- EM -- 7 1.00e+00 1.07e-03 -- --
#> 1 +5.255399164e-01 +4.382e-02 7 ------ ------ -- --
#> 2 +5.242991562e-01 +6.915e-03 4 1.00e+00 1.89e-02 5 1
#> 3 +5.242979895e-01 +7.551e-05 4 1.00e+00 4.60e-04 2 1
#> 4 +5.242979894e-01 -2.385e-06 4 1.00e+00 5.87e-06 2 1
#> Optimization took 0.00 seconds.
#> Convergence criteria met---optimal solution found.
# Use an initial g (this fixes mode and scale for ash priors):
normalmix.res <- ebnm_normal_scale_mixture(x, s, g_init = pn.res)
# Fix g and get different output (including a posterior sampler):
pn.res <- ebnm_point_normal(x, s, g_init = pn.res, fix_g = TRUE,
output = ebnm_output_all())
# Sample from the posterior:
pn.samp <- simulate(pn.res, nsim = 100)
# Quantiles and HPD confidence intervals can be obtained via sampling:
set.seed(1)
pn.quantiles <- quantile(pn.res, probs = c(0.1, 0.9))
pn.quantiles[1:5, ]
#> 10% 90%
#> [1,] 0.0000000 1.1914106
#> [2,] -1.0619459 0.1206053
#> [3,] 0.0000000 1.7507120
#> [4,] -0.1512883 0.9017663
#> [5,] 0.0000000 1.2735313
confint(pn.res, level = 0.8, parm = 1:5)
#> CI.lower CI.upper
#> [1,] -0.03860609 1.22003099
#> [2,] -1.05387886 0.06733079
#> [3,] -0.05568353 1.55045799
#> [4,] -0.06929657 1.08525964
#> [5,] -0.03277069 1.27950472
# Examples of usage of control parameter:
# point_normal uses nlm:
pn.res <- ebnm_point_normal(x, s, control = list(print.level = 1))
#> iteration = 0
#> Step:
#> [1] 0 0
#> Parameter:
#> [1] 0.0000000 0.6123253
#> Function Value
#> [1] 160.1828
#> Gradient:
#> [1] -0.6458203 1.6594072
#>
#> iteration = 5
#> Parameter:
#> [1] -0.06634847 0.48643374
#> Function Value
#> [1] 160.0995
#> Gradient:
#> [1] 5.052228e-06 -5.652389e-06
#>
#> Relative gradient close to zero.
#> Current iterate is probably solution.
#>
# unimodal uses mixsqp:
unimodal.res <- ebnm_unimodal(x, s, control = list(verbose = TRUE))
#> Running mix-SQP algorithm 0.3-54 on 201 x 7 matrix
#> convergence tol. (SQP): 1.0e-08
#> conv. tol. (active-set): 1.0e-10
#> zero threshold (solution): 1.0e-08
#> zero thresh. (search dir.): 1.0e-14
#> l.s. sufficient decrease: 1.0e-02
#> step size reduction factor: 7.5e-01
#> minimum step size: 1.0e-08
#> max. iter (SQP): 1000
#> max. iter (active-set): 8
#> number of EM iterations: 20
#> Computing SVD of 201 x 7 matrix.
#> Matrix is not low-rank; falling back to full matrix.
#> iter objective max(rdual) nnz stepsize max.diff nqp nls
#> 1 +7.073053156e-01 -- EM -- 7 1.00e+00 1.02e-01 -- --
#> 2 +6.300507676e-01 -- EM -- 7 1.00e+00 9.84e-02 -- --
#> 3 +5.856263291e-01 -- EM -- 7 1.00e+00 8.30e-02 -- --
#> 4 +5.605377271e-01 -- EM -- 7 1.00e+00 6.48e-02 -- --
#> 5 +5.463980593e-01 -- EM -- 7 1.00e+00 4.86e-02 -- --
#> 6 +5.383344434e-01 -- EM -- 7 1.00e+00 3.59e-02 -- --
#> 7 +5.336431001e-01 -- EM -- 7 1.00e+00 2.65e-02 -- --
#> 8 +5.308472577e-01 -- EM -- 7 1.00e+00 1.96e-02 -- --
#> 9 +5.291369016e-01 -- EM -- 7 1.00e+00 1.46e-02 -- --
#> 10 +5.280610563e-01 -- EM -- 7 1.00e+00 1.09e-02 -- --
#> 11 +5.273636428e-01 -- EM -- 7 1.00e+00 8.23e-03 -- --
#> 12 +5.268961570e-01 -- EM -- 7 1.00e+00 6.26e-03 -- --
#> 13 +5.265707094e-01 -- EM -- 7 1.00e+00 4.80e-03 -- --
#> 14 +5.263343276e-01 -- EM -- 7 1.00e+00 3.71e-03 -- --
#> 15 +5.261546016e-01 -- EM -- 7 1.00e+00 2.89e-03 -- --
#> 16 +5.260114829e-01 -- EM -- 7 1.00e+00 2.28e-03 -- --
#> 17 +5.258924899e-01 -- EM -- 7 1.00e+00 1.81e-03 -- --
#> 18 +5.257898363e-01 -- EM -- 7 1.00e+00 1.46e-03 -- --
#> 19 +5.256986728e-01 -- EM -- 7 1.00e+00 1.19e-03 -- --
#> 20 +5.256159886e-01 -- EM -- 7 1.00e+00 1.07e-03 -- --
#> 1 +5.255399164e-01 +4.382e-02 7 ------ ------ -- --
#> 2 +5.242991562e-01 +6.915e-03 4 1.00e+00 1.89e-02 5 1
#> 3 +5.242979895e-01 +7.551e-05 4 1.00e+00 4.60e-04 2 1
#> 4 +5.242979894e-01 -2.385e-06 4 1.00e+00 5.87e-06 2 1
#> Optimization took 0.00 seconds.
#> Convergence criteria met---optimal solution found.