Fine-mapping with SuSiE-ash and SuSiE-inf

This vignette demonstrates how to use the SuSiE-ash and SuSiE-inf models. We use a simulated data set with n = 1000 individuals, p = 5000 variants, and a complex genetic architecture combining 3 sparse, 5 oligogenic, and 15 polygenic effects.

Data

library(susieR)
data(unmappable_data)

X <- unmappable_data$X
y <- as.vector(unmappable_data$y)
b <- unmappable_data$beta

plot(abs(b), ylab = "Absolute Effect Size", pch = 16)
points(which(b != 0), abs(b[b != 0]), col = 2, pch = 16)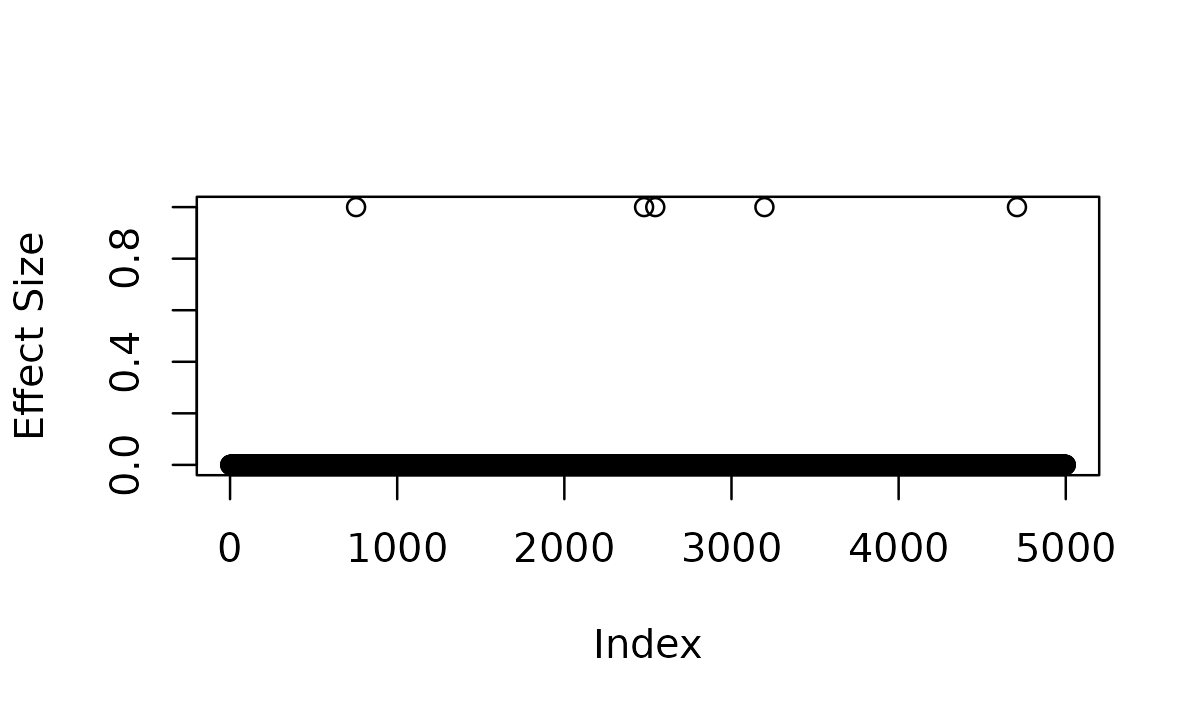

Summary Statistics and Z-Scores

Before fitting the models, we can examine the marginal association statistics. We use univariate_regression() to compute effect sizes and standard errors, then derive z-scores:

sumstats <- univariate_regression(X, y)
z_scores <- sumstats$betahat / sumstats$sebetahat

The z-scores show the strength of marginal association for each variant. Red points indicate non-zero effect sizes:

susie_plot(z_scores, y = "z", b = b, add_legend = TRUE)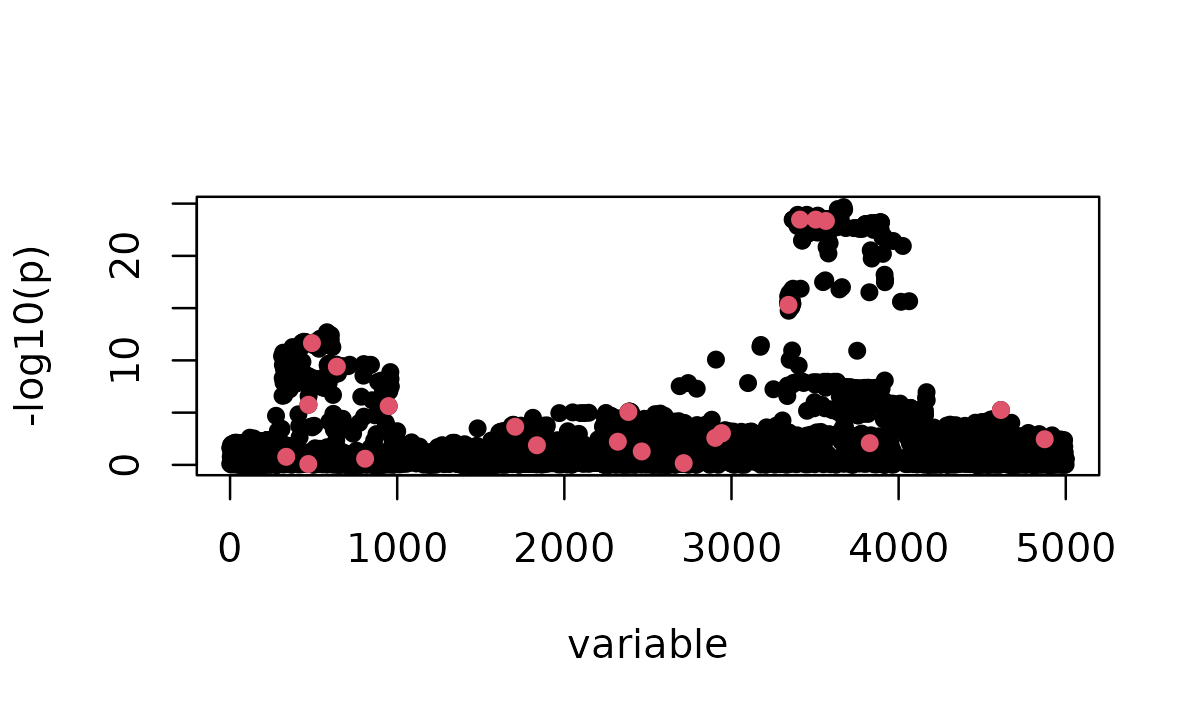

Here we can see the signal landscape before fine-mapping. Note that some causal variants have strong z-scores while others may be weaker or masked by LD with nearby variants.

Notably, variant 2714 has the largest true effect size in the simulation:

strongest_idx <- which.max(abs(b))
cat("Strongest effect variant:", strongest_idx, "\n")
# Strongest effect variant: 2714
cat("True effect size:", round(b[strongest_idx], 3), "\n")
# True effect size: -0.271
cat("Marginal z-score:", round(z_scores[strongest_idx], 3), "\n")
# Marginal z-score: -0.412
cat("Marginal p-value:", format.pval(2 * pnorm(-abs(z_scores[strongest_idx]))), "\n")
# Marginal p-value: 0.68011

Despite having the largest true effect, this variant has a very small marginal z-score and a large p-value. This illustrates a fundamental challenge in fine-mapping: the marginal association of a large-effect causal variant can be masked by other variants in LD, while smaller-effect variants may show stronger marginal signals. This masking makes it difficult to identify the true causal variants from marginal statistics alone.

Step 1: Standard SuSiE and False Positives

We first fit standard SuSiE:

t0 <- proc.time()
fit_susie <- susie(X, y, L = 10)
t1 <- proc.time()
t1 - t0
#    user  system elapsed 
#  47.739   0.036  12.334
susie_plot(fit_susie, y = "PIP", b = b, main = "SuSiE (standard)", add_legend = TRUE)

We set L = 10 to allow SuSiE to capture up to 10 sparse effects. However, given the complex architecture with 23 true causal variants, this may be insufficient.

To see which true effects the credible sets capture, we plot the CS on the true effect sizes:

plot_cs_effects <- function(fit, b, main = "") {
  colors <- c("dodgerblue2", "green4", "#6A3D9A", "#FF7F00", "gold1", "firebrick2")
  plot(abs(b), pch = 16, ylab = "Absolute Effect Size", main = main)
  if (!is.null(fit$sets$cs)) {
    for (i in rev(seq_along(fit$sets$cs))) {
      cs_idx <- fit$sets$cs[[i]]
      points(cs_idx, abs(b[cs_idx]), col = colors[(i-1) %% 6 + 1], pch = 16, cex = 1.5)
    }
  }
  
  cat(sprintf("True causals: %s\n", paste(which(b != 0), collapse=", ")))
  for (i in seq_along(fit$sets$cs)) {
    cs_idx <- fit$sets$cs[[i]]
    sentinel <- cs_idx[which.max(fit$pip[cs_idx])]
    tp <- any(b[cs_idx] != 0)
    cat(sprintf("  CS%d: %d %s\n", i, sentinel, ifelse(tp, "TP", "FP")))
  }
}

plot_cs_effects(fit_susie, b, main = "SuSiE CS on true effects")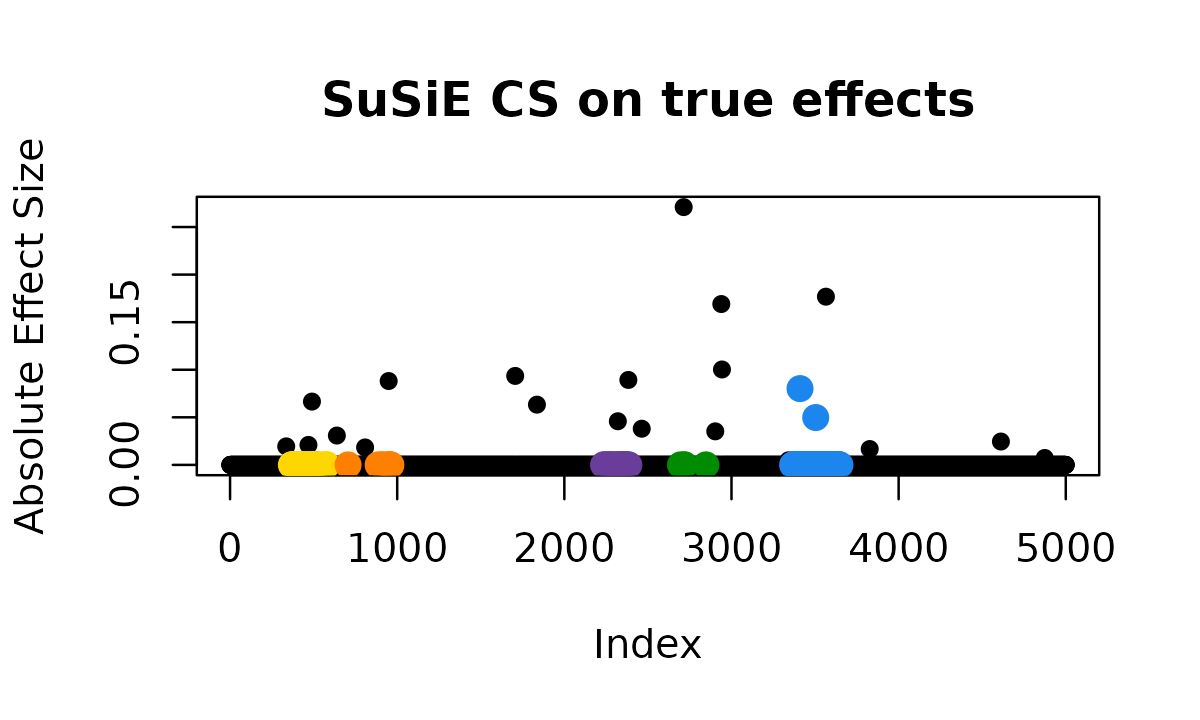

# True causals: 336, 468, 469, 490, 639, 808, 949, 1706, 1836, 2320, 2383, 2463, 2714, 2903, 2939, 2943, 3341, 3410, 3504, 3565, 3827, 4612, 4874
#   CS1: 3520 TP
#   CS2: 2716 FP
#   CS3: 2386 FP
#   CS4: 960 FP
#   CS5: 447 FP

SuSiE identifies 5 credible sets, but examining them more closely reveals a problem. Many of these credible sets appear to be false positives arising from synthetic associations.

A synthetic association occurs when a non-causal variant shows an association with the phenotype because it is in LD with true causal variants. The non-causal variant “borrows” signal from correlated effect variants, and when it is correlated with multiple effect variants, these contributions can accumulate to create an inflated signal.

Let’s examine one of the false positive credible sets to see this in action:

nonzero_idx <- which(b != 0)
fp_cs <- fit_susie$sets$cs[["L4"]]
top_var <- fp_cs[which.max(fit_susie$pip[fp_cs])]

cat("False positive CS top variant:", top_var, "\n")
# False positive CS top variant: 2716
cat("True effect (beta):", b[top_var], "\n")
# True effect (beta): 0
cat("Z-score:", round(z_scores[top_var], 2), "\n\n")
# Z-score: 3.89

cat("LD with true effect variants and their contributions:\n")
# LD with true effect variants and their contributions:
contributions <- data.frame(
  variant = nonzero_idx,
  r = round(sapply(nonzero_idx, function(v) cor(X[, top_var], X[, v])), 2),
  beta = round(b[nonzero_idx], 2)
)
contributions$r_times_beta <- round(contributions$r * contributions$beta, 2)
contributions <- contributions[order(-abs(contributions$r_times_beta)), ]
print(head(contributions[abs(contributions$r) > 0.1, ], 6), row.names = FALSE)
#  variant     r  beta r_times_beta
#     2714 -0.15 -0.27         0.04
#     2903  0.80  0.04         0.03
#     2939 -0.16 -0.17         0.03
#     3565  0.19 -0.18        -0.03
#     2943 -0.16 -0.10         0.02
#     3410  0.20 -0.08        -0.02

Variant 2716 has no true effect (beta = 0), yet it has a z-score of 3.89. This synthetic signal arises because it is correlated with multiple effect variants. Notice that:

It has negative LD with negative-effect variants (2714, 2939, 2943), giving positive contributions
It has positive LD with a positive-effect variant (2903), also giving a positive contribution

These contributions accumulate to create a synthetic signal at the non-causal variant, which SuSiE then incorrectly identifies as a distinct effect. The other false positive credible sets arise from the same artifact.

Step 2: Increasing Purity to Reduce False Positives

One approach to reduce false positives is to increase the purity threshold. By default, SuSiE uses min_abs_corr = 0.5. Let’s try min_abs_corr = 0.8:

cs_pure <- susie_get_cs(fit_susie, X = X, min_abs_corr = 0.8)
cat("Number of CSs with purity >= 0.8:", length(cs_pure$cs), "\n")
# Number of CSs with purity >= 0.8: 3

Raising the purity threshold removes some false positives, but not all of them. Some false positive credible sets have high purity because the non-causal variants within them are highly correlated with each other. These sets pass the purity filter yet still fail to contain any true causal variants.

Step 3: Fitting SuSiE-inf

SuSiE-inf models an infinitesimal component to account for unmappable effects:

t0 <- proc.time()
fit_inf <- susie(X, y, L = 10, unmappable_effects = "inf")
# WARNING: Unmappable effects models (inf/ash) do not have a well defined ELBO and require PIP convergence. Setting convergence_method='pip'.
# WARNING: Individual-level data will be converted to sufficient statistics for unmappable effects methods (this step may take a while for a large data set)
t1 <- proc.time()
t1 - t0
#    user  system elapsed 
# 260.125  12.164  95.127
susie_plot(fit_inf, y = "PIP", b = b, main = "SuSiE-inf", add_legend = TRUE)

(Note that it may take several minutes to fit the SuSiE-Inf model.)

plot_cs_effects(fit_inf, b, main = "SuSiE-inf CS on true effects")

# True causals: 336, 468, 469, 490, 639, 808, 949, 1706, 1836, 2320, 2383, 2463, 2714, 2903, 2939, 2943, 3341, 3410, 3504, 3565, 3827, 4612, 4874
#   CS1: 2714 TP

SuSiE-inf is more conservative and finds only 1 credible set, eliminating the false positives. However, it also loses the true signal around position 3500 that standard SuSiE correctly identified.

Remarkably, SuSiE-inf identifies the variant with the strongest true effect, the same variant we noted earlier has a very small marginal z-score and large p-value:

if (length(fit_inf$sets$cs) > 0) {
  inf_cs <- fit_inf$sets$cs[[1]]
  cat("SuSiE-inf CS contains variant", strongest_idx, ":", strongest_idx %in% inf_cs, "\n")
  cat("This variant has the largest true effect (beta =", round(b[strongest_idx], 3), 
      ") but marginal z-score of only", round(z_scores[strongest_idx], 3), "\n")
}
# SuSiE-inf CS contains variant 2714 : TRUE 
# This variant has the largest true effect (beta = -0.271 ) but marginal z-score of only -0.412

This is a striking, as SuSiE-inf recovers the strongest causal signal that is completely invisible in marginal statistics. The intuition is that by modeling background polygenic effects, SuSiE-inf effectively conditions on other variants, revealing signals that are otherwise masked.

However, for other signals, even if we lower the coverage threshold, we cannot recover them, potentially because SuSiE-inf was too aggressive removing them early-on in the SuSiE fit:

for (cov in c(0.9, 0.8, 0.7, 0.5)) {
  cs <- susie_get_cs(fit_inf, X = X, coverage = cov)
  cat(sprintf("Coverage=%.1f: %d credible sets\n", cov, length(cs$cs)))
}
# Coverage=0.9: 1 credible sets
# Coverage=0.8: 1 credible sets
# Coverage=0.7: 1 credible sets
# Coverage=0.5: 1 credible sets

Step 4: SuSiE-ash Achieves the Middle Ground

SuSiE-ash uses adaptive shrinkage to model the unmappable effects, providing a middle ground between standard SuSiE and SuSiE-inf:

t0 <- proc.time()
fit_ash <- susie(X, y, L = 10, unmappable_effects = "ash", verbose = TRUE)
# WARNING: Unmappable effects models (inf/ash) do not have a well defined ELBO and require PIP convergence. Setting convergence_method='pip'.
# WARNING: Individual-level data will be converted to sufficient statistics for unmappable effects methods (this step may take a while for a large data set)
# Mr.ASH terminated at iteration 20: max|beta|=4.0150e-03, sigma2=3.6691e-01, pi0=0.9811
# max |change in PIP|: 0.284002
# Mr.ASH terminated at iteration 15: max|beta|=3.2730e-03, sigma2=3.7297e-01, pi0=0.9876
# max |change in PIP|: 0.0340791
# Mr.ASH terminated at iteration 14: max|beta|=3.1126e-03, sigma2=3.7320e-01, pi0=0.9880
# max |change in PIP|: 0.0232019
# Mr.ASH terminated at iteration 13: max|beta|=3.1054e-03, sigma2=3.7327e-01, pi0=0.9879
# max |change in PIP|: 0.0122464
# Mr.ASH terminated at iteration 13: max|beta|=3.0981e-03, sigma2=3.7322e-01, pi0=0.9879
# max |change in PIP|: 0.00368497
# Mr.ASH terminated at iteration 13: max|beta|=3.1027e-03, sigma2=3.7326e-01, pi0=0.9879
# max |change in PIP|: 0.291487
# Mr.ASH terminated at iteration 13: max|beta|=3.0892e-03, sigma2=3.7328e-01, pi0=0.9878
# max |change in PIP|: 0.0640529
# Mr.ASH terminated at iteration 13: max|beta|=3.1078e-03, sigma2=3.7322e-01, pi0=0.9880
# max |change in PIP|: 0.0191625
# Mr.ASH terminated at iteration 13: max|beta|=3.1096e-03, sigma2=3.7324e-01, pi0=0.9881
# max |change in PIP|: 0.00238849
# Mr.ASH terminated at iteration 13: max|beta|=3.1120e-03, sigma2=3.7327e-01, pi0=0.9881
# max |change in PIP|: 0.00082723
t1 <- proc.time()
t1 - t0
#    user  system elapsed 
# 153.076   5.682  69.282
susie_plot(fit_ash, y = "PIP", b = b, main = "SuSiE-ash", add_legend = TRUE)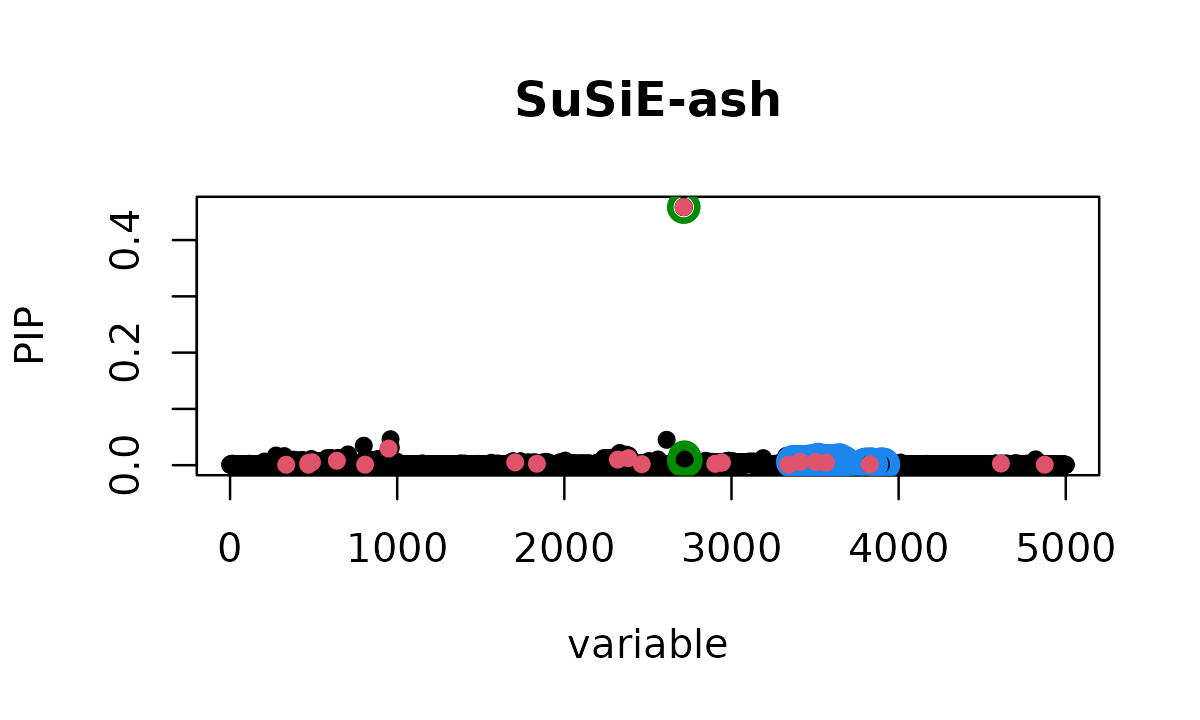

(Note that it may take several minutes to fit the SuSiE-ash model.)

plot_cs_effects(fit_ash, b, main = "SuSiE-ash CS on true effects")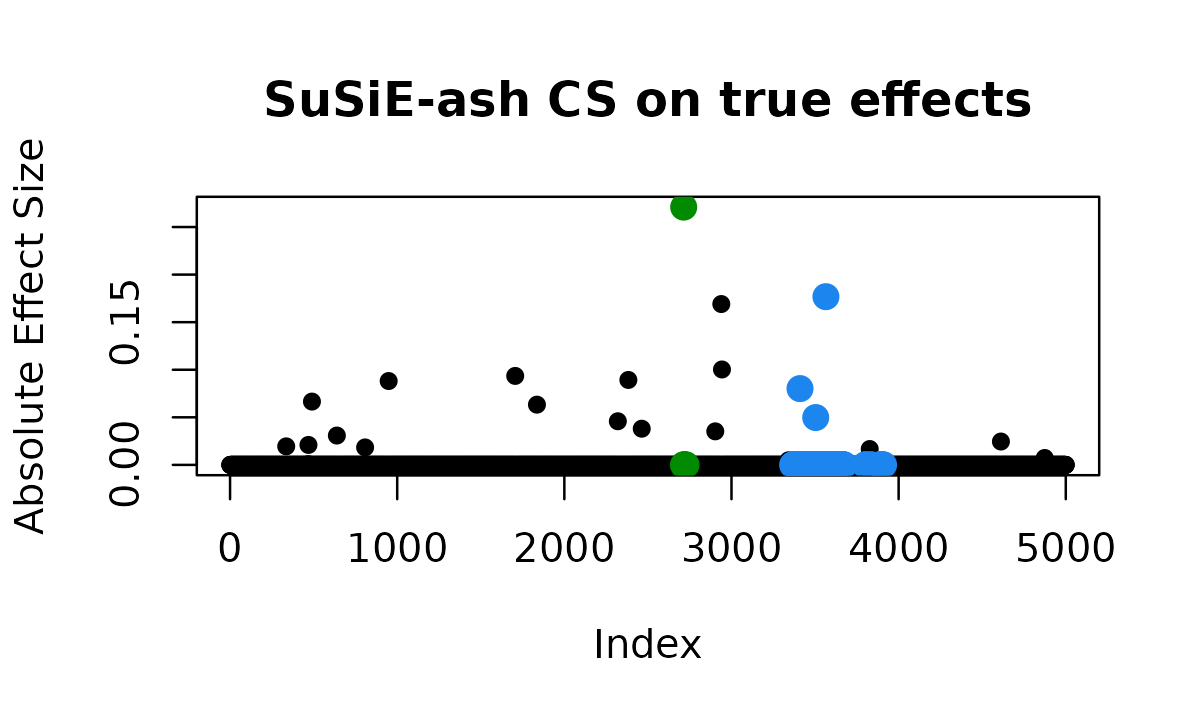

# True causals: 336, 468, 469, 490, 639, 808, 949, 1706, 1836, 2320, 2383, 2463, 2714, 2903, 2939, 2943, 3341, 3410, 3504, 3565, 3827, 4612, 4874
#   CS1: 3671 TP
#   CS2: 603 TP
#   CS3: 2386 TP

SuSiE-ash finds 3 correct credible sets.

Still, it does not discover all 23 causal variants, nor does it recover the strongest effect (variant 2714) that SuSiE-inf found. However, the adaptive shrinkage approach allows SuSiE-ash to distinguish between true sparse signals and the polygenic background more effectively than either standard SuSiE or SuSiE-inf alone.

Summary

Method	Credible Sets	False Positives
SuSiE (purity=0.5)	5	4
SuSiE (purity=0.8)	3	2
SuSiE-inf	1	0
SuSiE-ash	3	0

What if we increase L for standard SuSiE?

Since the true simulation has 23 causal variants, one might ask: what if we simply increase L to give SuSiE more capacity? Let’s try L = 40:

t0 <- proc.time()
fit_susie_L40 <- susie(X, y, L = 40)
t1 <- proc.time()
t1 - t0
#    user  system elapsed 
# 295.250   0.527  74.390
susie_plot(fit_susie_L40, y = "PIP", b = b, main = "SuSiE (L=40)", add_legend = TRUE)

plot_cs_effects(fit_susie_L40, b, main = "SuSiE L=40 CS on true effects")

# True causals: 336, 468, 469, 490, 639, 808, 949, 1706, 1836, 2320, 2383, 2463, 2714, 2903, 2939, 2943, 3341, 3410, 3504, 3565, 3827, 4612, 4874
#   CS1: 3520 TP
#   CS2: 2716 FP
#   CS3: 580 TP
#   CS4: 2386 FP

With L = 40, standard SuSiE does improve! Now it captures 4 CS with two of them true positives. However, it still produces false positives and takes considerably longer to converge.

The rationale for SuSiE-ash is to avoid this concern: rather than specifying a large L to account for all potential effects, we use a reasonable L for sparse signals and let the adaptive shrinkage component absorb effects that cannot be mapped due to insufficiently specified L. This provides a more principled and computationally efficient approach.

Naturally as a result, SuSiE-ash is more robust to the choice of L compared to SuSiE. For this example, setting L anywhere from 5 to 40 yields similar results, unlike standard SuSiE where performance varies substantially with L. (Readers can verify this on their own with this data-set)

Session Information

sessionInfo()
# R version 4.4.3 (2025-02-28)
# Platform: x86_64-conda-linux-gnu
# Running under: Ubuntu 24.04.3 LTS
# 
# Matrix products: default
# BLAS/LAPACK: /home/runner/work/susieR/susieR/.pixi/envs/r44/lib/libopenblasp-r0.3.30.so;  LAPACK version 3.12.0
# 
# locale:
#  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
# [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
# 
# time zone: Etc/UTC
# tzcode source: system (glibc)
# 
# attached base packages:
# [1] stats     graphics  grDevices utils     datasets  methods   base     
# 
# other attached packages:
# [1] susieR_0.15.4
# 
# loaded via a namespace (and not attached):
#  [1] Matrix_1.7-4          gtable_0.3.6          jsonlite_2.0.0       
#  [4] compiler_4.4.3        crayon_1.5.3          Rcpp_1.1.1           
#  [7] jquerylib_0.1.4       systemfonts_1.3.1     scales_1.4.0         
# [10] textshaping_1.0.4     yaml_2.3.12           fastmap_1.2.0        
# [13] lattice_0.22-7        plyr_1.8.9            ggplot2_4.0.1        
# [16] R6_2.6.1              mixsqp_0.3-54         knitr_1.51           
# [19] htmlwidgets_1.6.4     zigg_0.0.2            desc_1.4.3           
# [22] bslib_0.9.0           RColorBrewer_1.1-3    rlang_1.1.7          
# [25] cachem_1.1.0          reshape_0.8.10        xfun_0.55            
# [28] fs_1.6.6              sass_0.4.10           S7_0.2.1             
# [31] RcppParallel_5.1.11-1 otel_0.2.0            cli_3.6.5            
# [34] pkgdown_2.2.0         digest_0.6.39         grid_4.4.3           
# [37] irlba_2.3.5.1         lifecycle_1.0.5       vctrs_0.6.5          
# [40] Rfast_2.1.5.2         evaluate_1.0.5        glue_1.8.0           
# [43] farver_2.1.2          ragg_1.5.0            rmarkdown_2.30       
# [46] matrixStats_1.5.0     tools_4.4.3           htmltools_0.5.9

Alex McCreight

2026-01-17