Fit Empirical Bayes Matrix Factorization

This is the main interface for fitting EBMF models based on algorithms from Wang and Stephens. The default behaviour is simply to run the greedy algorithm and return the result. To follow it by backfitting set backfit = TRUE.

flash(data, Kmax = 100, f_init = NULL, var_type = c("by_column", "by_row",
  "constant", "zero", "kroneker"), init_fn = "udv_si", tol = 0.01,
  ebnm_fn = ebnm_pn, ebnm_param = flash_default_ebnm_param(ebnm_fn),
  verbose = FALSE, nullcheck = TRUE, seed = 123, greedy = TRUE,
  backfit = FALSE)

Arguments

data	An n by p matrix or a flash data object created using flash_set_data.
Kmax	The maximum number of factors to be added to the flash object. (If nullcheck = TRUE, the actual number of factors added might be less than Kmax.)
f_init	The flash object to which new factors are to be added. If f_init = NULL, then a new flash fit object is created.
var_type	The type of variance structure to assume for residuals.
init_fn	The function used to initialize factors. This function should take parameters (Y,K) where Y is an n by p matrix of data (or a flash data object) and K is a number of factors. It should output a list with elements (u,d,v) where u is n by K matrix v is a p by K matrix and d is a K vector. See udv_si for an example. (If the input data includes missing values then this function must be able to deal with missing values in its input matrix.)
tol	Specifies how much the objective can change in a single iteration to be considered not converged.
ebnm_fn	The function used to solve the Empirical Bayes Normal Means problem.
ebnm_param	A named list containing parameters to be passed to ebnm_fn when optimizing; defaults are set by flash_default_ebnm_param().
verbose	If TRUE, various progress updates will be printed.
nullcheck	If TRUE, then after running hill-climbing updates, flash will check whether the achieved optimum is better than setting the factor to 0. If the check is performed and fails then the factor will be set to 0 in the returned fit.
seed	A random number seed to use before running flash - for reproducibility. Set to NULL if you don't want the seed set. (The seed can affect initialization when there are missing data; otherwise the algorithm is deterministic.)
greedy	If TRUE, factors are added via the greedy algorithm. If FALSE, then f_init must be supplied.
backfit	If TRUE, factors are refined via the backfitting algorithm.

Value

A fitted flash object. Use flash_get_ldf to access standardized loadings and factors; use flash_get_lf to access fitted LF'.

See also

flash_add_greedy, flash_backfit

Examples

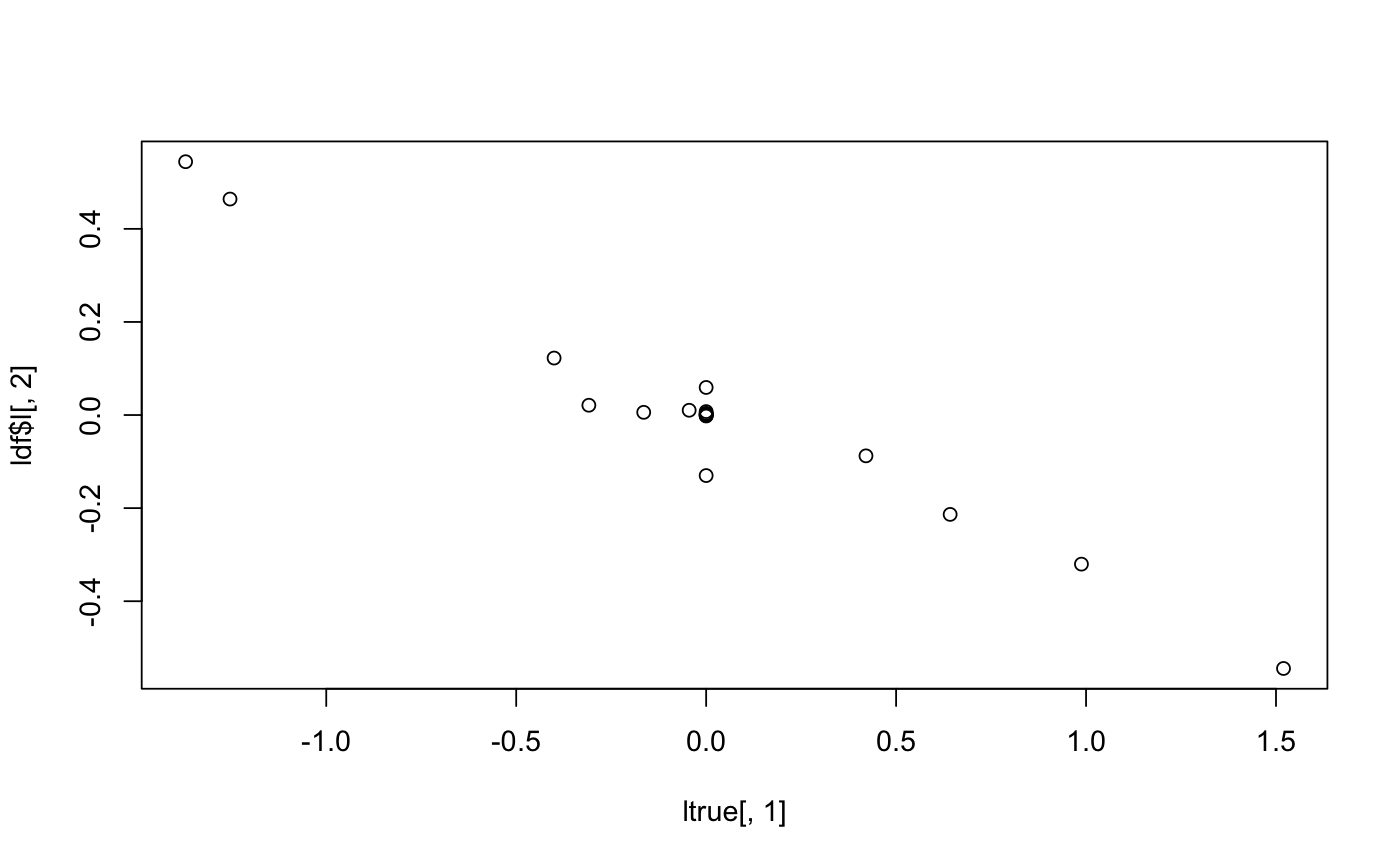
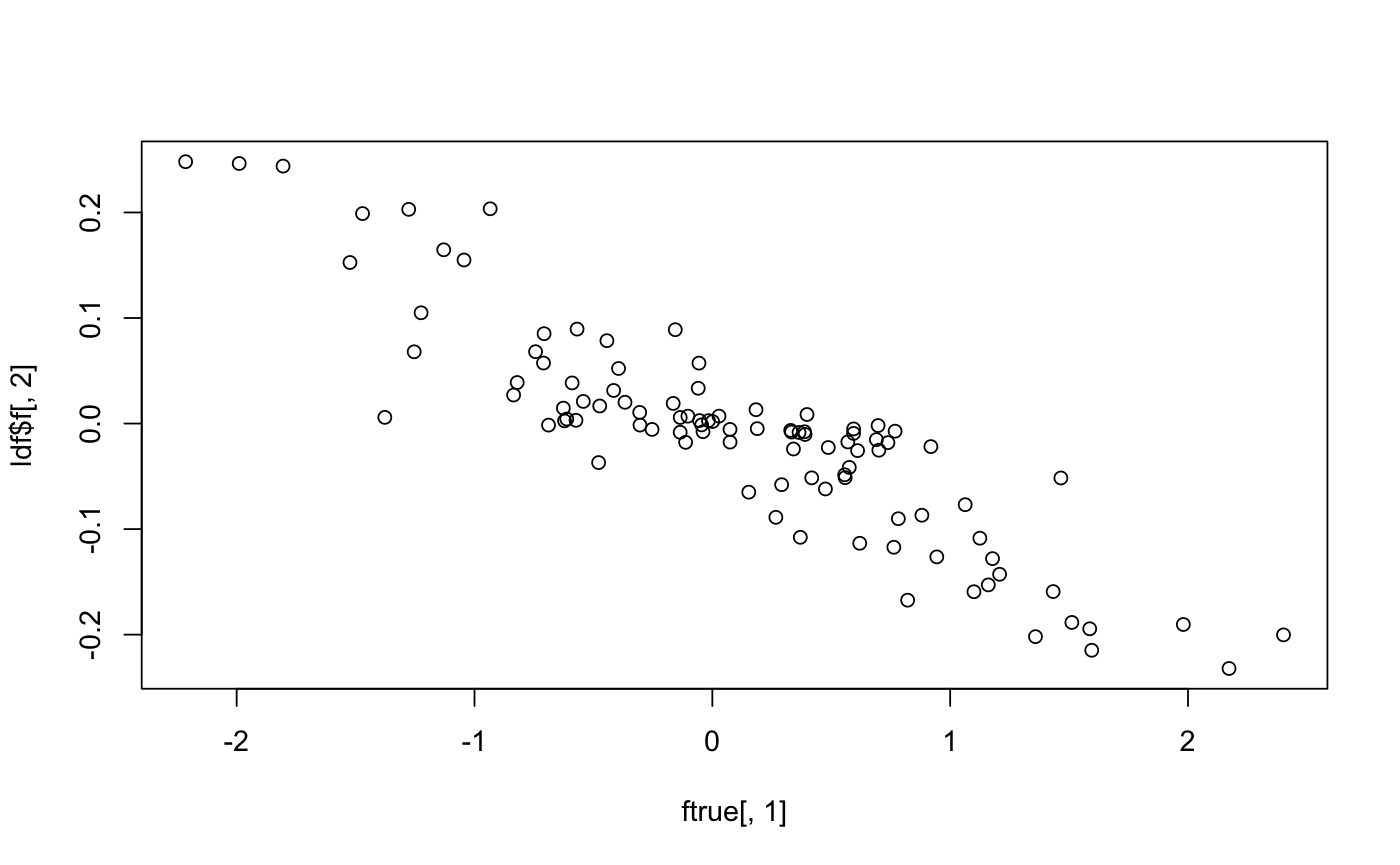
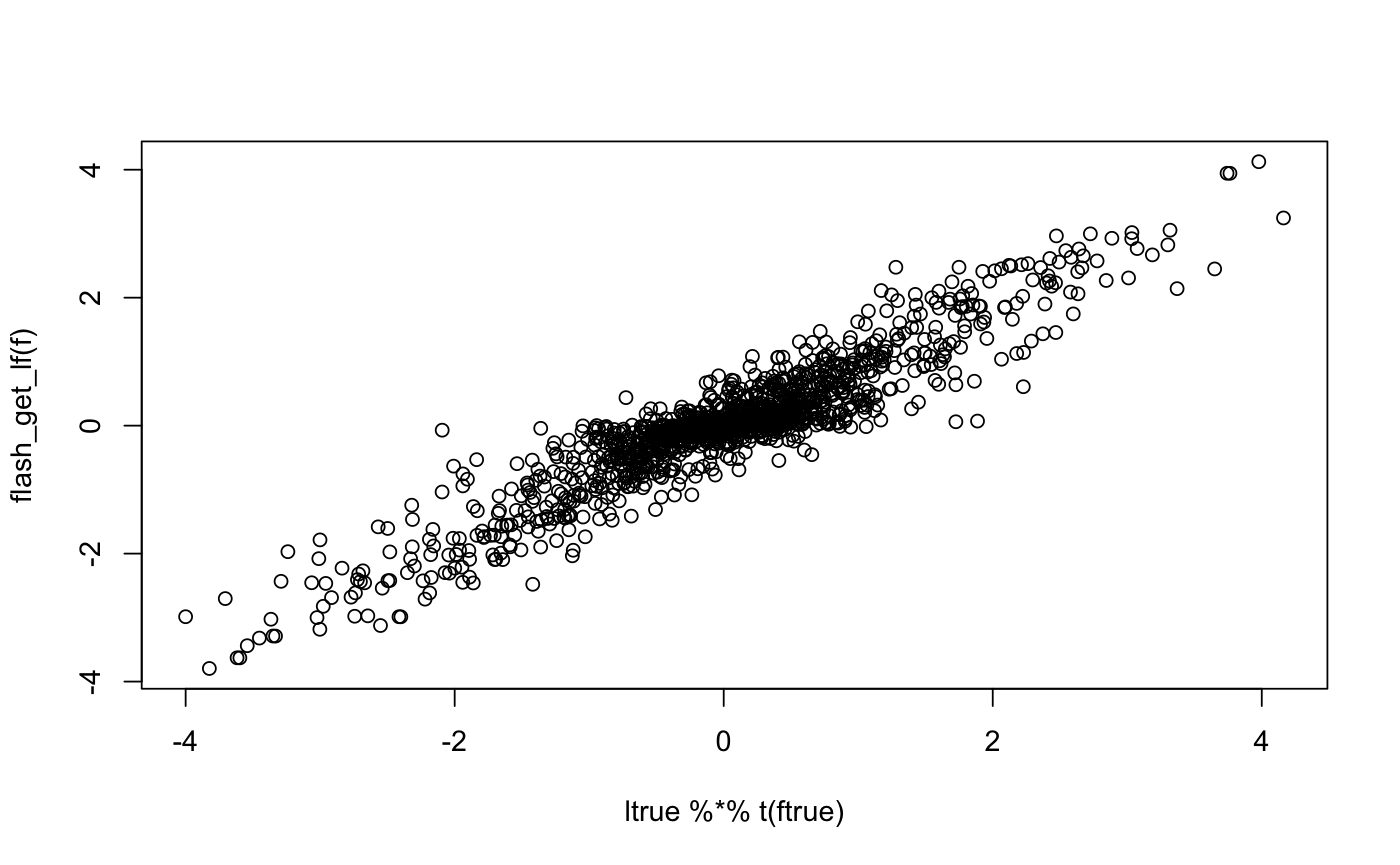
set.seed(1) # for reproducibility
ftrue = matrix(rnorm(200),ncol=2)
ltrue = matrix(rnorm(40),ncol=2)
ltrue[1:10,1] = 0 # set up some sparsity
ltrue[11:20,2] = 0
Y = ltrue %*% t(ftrue)+rnorm(2000) # set up a simulated matrix
f = flash(Y)
#> fitting factor/loading 1
#> fitting factor/loading 2
#> fitting factor/loading 3
ldf = flash_get_ldf(f)

# Show the weights, analogous to singular values showing importance
# of each factor.
ldf$d
#> [1] 29.16 22.36

# Plot true l against estimated l; with this seed it turns out the
# 2nd loading/factor corresponds to the first column of ltrue.
plot(ltrue[,1],ldf$l[,2])

# Plot true f against estimated f (note estimate is normalized).
plot(ftrue[,1],ldf$f[,2])

# Plot true lf' against estimated lf'; the scale of the estimate
# matches the data.
plot(ltrue %*% t(ftrue), flash_get_lf(f))

# Example to use the more flexible ebnm function in ashr.
f2 = flash(Y,ebnm_fn = ebnm_ash)
#> fitting factor/loading 1
#> fitting factor/loading 2
#> fitting factor/loading 3

# Example to show how to pass parameters to ashr (may be most
# useful for research use).
f3 = flash(Y,ebnm_fn = ebnm_ash,
           ebnm_param = list(mixcompdist = "normal",method="fdr"))
#> fitting factor/loading 1
#> fitting factor/loading 2
#> fitting factor/loading 3

# Example to show how to use a different initialization function.
library(softImpute)
f4 = flash(Y,init_fn = function(x,K=1){softImpute(x,K,lambda=10)})
#> fitting factor/loading 1
#> fitting factor/loading 2
#> fitting factor/loading 3